Начать разбираться в сущности спектральных представлений лучше с разложения в ряд Фурье периодического сигнала. Всякая периодическая функция (с ограничениями, носящими абстрактный характер) может быть представлена в виде разложения в ряд по тригонометрическим функциям

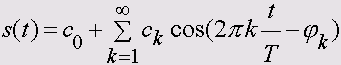(1.1)

Таким образом, периодическая функция s(t) представлена суммой слагаемых, каждое из которых есть не что иное, как косинусоидальное колебание с амплитудой сk и начальной фазой .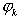
Совокупность коэффициентов сk называется амплитудным спектром сигнала, а 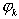— фазовым спектром.
Частоты всех синусоидальных колебаний, из которых составляется периодическая функция s(t), кратны основной частоте F =1/Т. Отдельные составляющие называются гармониками. Колебание с частотой F называется первой гармоникой (k = 1), с частотой 2F— второй гармоникой (k = 2) и т. д.
Ряд Фурье дает разложение периодической функции по тригонометрическим функциям. Это разложение можно применить и к непериодической функции, которую рассматривают как предельный случай периодической функции при неограниченном возрастании периода.
Если Т->, то F-> df, a 2pk/T-> w (параметр w— круговая текущая частота, изменяющаяся непрерывно). Не хотелось бы здесь рассказывать подробно обо всех математических преобразованиях, которые необходимо выполнить при таком предельном переходе. Поэтому сразу приведем итоговые формулы, которые являются основными соотношениями теории спектров. Они представляют собой пару преобразований Фурье, связывающих между собой две функции: вещественную функцию времени s(t) и комплексную функцию частоты G(w):

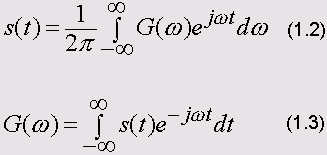
Формула (1.2) называется интегралом Фурье в комплексной форме. В данном случае предполагается, что функция непериодическая, поэтому она может быть представлена только суммой бесконечно большого числа бесконечно близких по частоте колебаний с бесконечно малыми амплитудами.
Если ряд Фурье представляет периодическую функцию суммой хотя и бесконечного числа синусоид, но с частотами, имеющими определенные дискретные значения, то интеграл Фурье представляет непериодическую функцию суммой синусоид и косинусоид с непрерывной последовательностью частот. Иногда говорят, что в .составе непериодического сигнала есть колебания всех частот. В случае непериодического сигнала говорить об амплитудах отдельных спектральных составляющих нет смысла, т. к. это бесконечно малые величины. На самом деле параметр G(w) выражает не непосредственно амплитуду, а так называемую спектральную плотность. Обычно эту деталь опускают и называют G(w) комплексным спектром непериодической функции, а абсолютное значение этой величины — просто спектром.
В специальной литературе можно найти теоремы, позволяющие облегчить спектральные преобразования сигналов, а также соотношения и графики, описывающие спектры сигналов различной формы.

Текущий спектр

Классическое определение спектра основывается на преобразовании Фурье, причем интегрирование по времени выполняется в бесконечных пределах и спектр зависит только от частоты. Однако бесконечная длительность какого-либо процесса — это абстракция, не имеющая ничего общего с реальностью.
Если анализируемая функция есть отображение некоторого реального физического процесса, то сведения о функции С(w) мы получаем лишь в результате наших наблюдений. Следовательно, при вычислении спектра мы можем выполнить интегрирование лишь от момента начала анализа до текущего момента времени t, а не до момента, устремленного в бесконечное будущее.
Текущий спектр определяется как результат преобразования Фурье, но с переменным верхним пределом интегрирования, в качестве которого фигурирует текущее время. Поэтому текущий спектр является функцией не только частоты, но и времени.
В начале раздела мы воспользовались понятием периодической функции. На самом деле периодическая функция — лишь весьма полезная математическая абстракция. Ведь всякий природный процесс имеет начало и конец.
Принято называть реальный циклический процесс периодическим, если он длится достаточно долго. Мерилом длительности служит число "периодов", которое должно быть намного больше единицы. Периодичность процесса проявляется лишь с течением времени, когда прорисовываются его характерные черты. Текущий спектр и отражает это развитие процесса.
Спектр процесса (за короткий отрезок времени) однороден, так как короткий отрезок процесса — это просто короткий одиночный импульс. Если в дальнейшем происходит периодическое повторение некоторого цикла явления, то в текущем спектре начинают формироваться максимумы на основной частоте и ее гармониках. Эти пики становятся все более острыми и высокими, а значение спектральной плотности в интервалах между максимумами убывает, и при t -> сплошной текущий спектр вырождается в линейчатый спектр периодического процесса.
Конечно, и при достаточно большой (не обязательно бесконечной) длительности процесса пики делаются настолько узкими, что их можно трактовать как линии.
Таким образом, периодический процесс — это предел, к которому может стремиться с течением времени реальный повторяющийся процесс. Аналогично и спектр (в его классическом определении) такого процесса есть предел, к которому стремится текущий спектр при увеличении времени интегрирования до бесконечности.
Например, при интегрировании в бесконечных пределах спектр синусоиды представляет собой единственную линию на частоте, равной частоте этой синусоиды.
Но как на практике измеряется текущий спектр, например, той же синусоиды? Мы включаем анализатор спектра, а спустя какое-то время выключаем его. Получается, что измеряется не спектр бесконечного синусоидального колебания, а спектр его более или менее протяженного отрезка. Это значит, что фактически исследуется спектр прямоугольного импульса с синусоидальным заполнением. Сказанное объясняет причину того, что даже для синусоидального колебания при уменьшении времени интегрирования спектральная линия расширяется, появляются боковые лепестки спектральной функции, ее нули все более удаляются друг от друга. Ведь именно так и должен вести себя спектр прямоугольного импульса при уменьшении его длительности.
Таким образом, текущий спектр в большей степени отражает свойства сигналов, проявляющиеся в реальных условиях их генерирования и обработки, нежели спектр, полученный на бесконечном временном интервале.

Мгновенный спектр

Текущий спектр — только мостик от частотного к временному описанию процесса. Представьте себе, что вы анализируете текущий спектр от начала до конца музыкального произведения, не слыша его. Вполне возможно, вы получите такой график спектральной функции, что в среднем за время анализа спектр будет выглядеть относительно широким. Рассматривая график, можно прийти, например, к следующему выводу: произведение исполняется одновременно на нескольких инструментах. В тембре звучания одних инструментов преобладают низкочастотные, других — средне- и высокочастотные составляющие.
Потом вы выводите сигнал на акустическую систему и оказывается, что это запись дуэта мужчины и женщины в сопровождении фортепиано. На самом деле тембр звука периодически меняется. Пока звучит баритон, в нем преобладают бархатные низкочастотные составляющие, а когда диалог продолжает сопрано, кажется, что звенит колокольчик. Но все эти нюансы оказались усреднены, сглажены, завуалированы в ходе спектрального анализа.
Для чего же нужны тогда все эти измерения спектра, если они не дают достоверной картины реального развития тембра музыкального произведения? На основе такого анализа трудно построить детальную стратегию последующей обработки фонограммы. Все дело в том, что не только спектр, вычисленный на бесконечном временном интервале, но и текущий спектр — слишком грубый инструмент в тех случаях, когда анализируемый процесс не стационарен. Для того чтобы сблизить частотное и временное представления сигнала, было введено понятие мгновенный спектр. Мгновенный спектр — это спектр короткого отрезка процесса длительностью T, непосредственно предшествующего данному моменту времени t.
В этом определении мы имеем дело со скользящим интегрированием: интервал интегрирования имеет постоянную длину, но перемещается по оси времени. А вот относительно текущего времени этот интервал расположен неизменно.
Страшно далеко это определение спектра от того, что давно придумали великие математики. И все же в руках звукорежиссера именно мгновенный спектр является наиболее эффективным инструментом анализа свойств записываемого или уже записанного звука. Все дело в том, что реальные звуковые сигналы, с которыми нам приходится сталкиваться, одинаково непохожи на обе крайние математические абстракции — бесконечное во времени сверхузкополосное синусоидальное колебание и бесконечный в частотной области (сверхширокополосный) белый шум.
Музыка, которую создают с помощью синтезатора, отличается особенно заметной нестационарностью тембра. Может быть, именно поэтому в звуковых редакторах уже давно используются средства анализа текущего и мгновенного спектра.

Взвешенный спектр

Вы познакомились с тремя подходами к вычислению спектра и даже вынуждены были вникать в непростые математические соотношения. Но это еще не финал. Продолжим погружение в суть спектральных преобразований. И вновь речь пойдет о влиянии времени на результаты спектрального анализа.
Как вычисляется одна-единственная точка графика спектра? Исчерпывающий ответ на этот вопрос дают формулы. Хочется, однако, чтобы их вид не приводил вас в состояние трепета. Главное, чтобы вы понимали их смысл, поэтому попытаемся разъяснить обычными словами то, что записано математическими символами.
Итак, сначала выбирается частота f0. Реальный или виртуальный генератор формирует синусоиду этой частоты и условно единичной амплитуды. Исследуемый сигнал нормируется по амплитуде. Начиная с какого-то определенного момента f0, с шагом t (чем меньше t, тем лучше) в моменты времени t0, t1, t2, t3,...ti,...,tN-1 c этой синусоидой и исследуемым сигналом проделываются следующие операции:

* берется отсчет синусоиды;
* берется отсчет исследуемого сигнала;
* эти отсчеты перемножаются;
* результаты перемножения суммируются с накоплением.

В некоторый момент процесс измерения спектра на частоте f0 завершается. Накопленная сумма делится на общее число отсчетов. Вычисленное значение G(f0) запоминается и, возможно, отображается как одна точка графика. Затем накопленная сумма обнуляется, значение частоты изменяется на величину f (выбирается новое значение частоты f1). И вся последовательность операций повторяется до тех пор, пока "пробежкой" по ряду частот f0,f1,f2,...,fN-1 не будет перекрыт весь заданный диапазон.
Описанная процедура вычисления спектрального коэффициента одновременно есть не что иное, как вычисление взаимокорреляционной функции исследуемого сигнала и синусоиды заданной частоты. Иными словами, в процессе вычисления спектральной составляющей выясняется степень сходства исследуемого сигнала со стандартным (базисным) сигналом, в данном случае с синусоидой. Или можно сказать еще и так: выясняется, в какой пропорции синусоида "содержится" в исследуемом сигнале.
Если исследуемый сигнал уже записан и в нашем распоряжении есть цифровой анализатор спектра, способный сколь угодно долго хранить результаты промежуточных вычислений, то измерение текущего спектра и мгновенного спектра вполне осуществимо по описанной выше процедуре.
Все значительно сложнее, когда анализ ведется в реальном времени. В самом деле, допустим, что одна спектральная составляющая вычислена. Изменяем частоту синусоиды и хотим приступить к вычислению следующей спектральной составляющей. Но анализируемый фрагмент сигнала остался в прошлом. Его не повторить. Поэтому вторая спектральная составляющая будет вычислена для второго фрагмента сигнала, третья — для третьего и т. д. Это уже не текущий спектр, а просто разрозненный набор отдельных спектральных коэффициентов, каждый из которых в ничтожно малой степени характеризует совершенно разные и, возможно, не связанные между собой фрагменты сигнала.
Конечно, спектральный анализ можно проводить по параллельной схеме, одновременно вычисляя множество значений спектральной функции для различных частот. Однако это в значительной степени усложнит аппаратуру.
Уместен и такой вопрос: насколько адекватен описанный математический алгоритм тому спектральному анализу, который проводится реальными анализаторами спектра, и тому, который выполняется органами слуха и мозгом человека? Ответ: не вполне.
Основная проблема состоит в том, что прибор, анализирующий спектр, и человек обладают конечной памятью. Былые события, подробности хода любого процесса постепенно стираются из нее. Это означает, что чем более удалены в прошлое отсчеты анализируемого сигнала, тем меньший вклад они вносят в накопление той самой суммы произведений отсчетов, которая, в конце концов, определяет значение спектрального коэффициента.
Учет реальных свойств памяти анализаторов спектра осуществляется с помощью весовых функций. Весовая функция описывает зависимость вклада предшествующих отсчетов исследуемого сигнала в вычисляемый спектр. Наглядное представление о весовой функции дает форма так называемого спектрального окна.
Тот спектральный анализ, о котором мы вели речь до сих пор, соответствует спектральному окну прямоугольной формы: весовая функция равна единице в пределах спектрального окна и равна нулю вне его. При анализе текущего спектра начало спектрального окна совпадает с началом отсчета времени, а конец приходится на текущий момент. Текущее время идет вперед, правая граница спектрального окна смещается, поэтому каждому конкретному моменту завершения анализа соответствует своя ширина спектрального окна. Если вычисляется мгновенный спектр, то спектральное окно скользит вдоль оси времени, не изменяя своей ширины.
Однако в большей степени суть реального спектрального анализа отражает экспоненциальная весовая функция. Кстати говоря, экспонента и синусоида — прямо-таки магические функции. Многие существующие в природе колебательные процессы описываются экспонентой при их возникновении и затухании, а синусоидой — на этапе продолжительного существования. В частности, по экспоненциальному закону затухают колебания в колебательном контуре, который служит основой реальных анализаторов спектра, т. е. как раз по экспоненте колебательный контур "забывает" величину спектральной составляющей, некогда возбудившей его. И именно по экспоненциальному закону стирается в памяти человека информация о прошедших событиях. Прямоугольное и экспоненциальное спектральные окна используется при вычислении спектра наиболее часто. Первое соответствует идеальному анализатору с бесконечно большой памятью, второе удачно отражает свойства человеческого мозга и реальных анализаторов спектра на основе резонансных фильтров. Вместе с тем, хотя не столь широко, применяются и другие весовые функции. Трудно дать конкретные рекомендации по поводу предпочтительности использования той или иной весовой функции для спектрального анализа звуковых сигналов (за исключением экспоненциальной функции, о пользе которой сказано уже достаточно). Пожалуй, единственный совет может состоять в том, что следует остановиться на какой-то одной весовой функции. Только тогда у вас будет уверенность в том, что различия результатов анализа обусловлены различием свойств сигналов, а не методов расчета. Целесообразно также выбирать одну и ту же весовую функцию, когда при работе с одним и тем же сигналом вы решаете несколько задач, в которых применяются спектральные преобразования.

Быстрое преобразование Фурье До сих пор, знакомясь с сущностью спектральных представлений, мы предполагали, что сигнал является аналоговым, т. е. описывается непрерывной функцией. На самом деле компьютер способен обрабатывать только цифровые сигналы — дискретные во времени и квантованные по уровню. Поэтому аналоговый сигнал подвергается аналого-цифровому преобразованию (АЦП). Затем с сигналом в цифровой форме производятся все необходимые операции, в частности, спектральный анализ, причем вместо обычного спектрального преобразования производится так называемое дискретное преобразование Фурье (ДПФ). Непрерывное время и непрерывная частота заменяются на соответствующие дискретные величины, а место взятия интегралов осуществляется суммирование. Однако на практике мало кто пользуется ДПФ. Дело в том, что для вычисления дискретного преобразования Фурье последовательности N элементов требуется выполнить N2 операций с комплексными числами. Если длины обрабатываемых массивов цифровых отсчетов звуковых колебаний имеют порядок тысячи и более, то использовать эти алгоритмы дискретного спектрального анализа затруднительно (особенно в реальном времени). Выходом из положения явился алгоритм быстрого преобразования Фурье (БПФ). Значительно сократить число выполняемых операций здесь удается за счет того, что обработка входного массива сводится к нахождению ДПФ-массивов с меньшим числом элементов. Для метода БПФ существенно, что число отсчетов составляет целую степень двойки (N =2p, где р — целое число). Это обусловлено тем, что одной из операций, входящей в алгоритм БПФ, является последовательное деление интервала вычисления ДПФ на две части. Поэтому точное вычисление БПФ возможно лишь в случае, когда число отсчетов в сигнале равно 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, IP. Если данное условие не выполняется, приходится дополнять сигнал некоторым количеством отсчетов, имеющих нулевое значение. Например, для выполнения БПФ сигнал, содержащий 60 значащих отсчетов, нужно дополнить четырьмя нулевыми отсчетами. Конечно, приписка отсчетов равноценна изменению сигнала, что приводит к возникновению дополнительной погрешности вычисления спектра. Но, как правило, погрешность невелика и, учитывая заметное повышение скорости расчетов, с ней можно смириться. Приближенно можно считать, что объем вычислений по алгоритму БПФ пропорционален произведению N х log2N, где N — количество отсчетов сигнала. А если решать задачу расчета спектра "в лоб", не пользуясь алгоритмами быстрых преобразований, то объем вычислений ориентировочно будет пропорционален произведению N х N. Если бы не БПФ, то для фильтрации, спектрального анализа и синтеза сигналов не хватило бы быстродействия самого современного компьютера. Не верится? Давайте прикинем. Очень скоро вы узнаете, что в примере установок параметров, соответствующих рис. 1.27, сигнал представлен 4096-ю отсчетами. Тогда для БПФ: 4096 х log24096 = 4096 х 12 = 49152, а для "небыстрого" алгоритма: 4096 х 4096 = 16777216. Отношение 16777216/49152 = 341,(3) приблизительно равно выигрышу во времени выполнения вычислений по алгоритму БПФ. О чем говорят эти цифры? Пусть на вашем компьютере для расчета фильтра по алгоритму БПФ требуется 10 секунд. Та же самая задача при использовании обычного алгоритма спектрального анализа заняла бы почти час. Какое уж тут может быть творчество! Либо, чтобы все-таки уложиться в 10 секунд, потребовался бы компьютер, работающий в 341 раз быстрее, чем ваш. При расчете спектра протяженных сигналов приходится не дополнять отсчеты до целой степени двойки, а поступать совершенно наоборот: использовать для вычислений не все отсчеты сигнала, а, к примеру, каждый сотый, тысячный, десятитысячный. Судите сами. В одной секунде оцифрованного стереофонического звука при частоте дискретизации 44,1 кГц содержится 88200 отсчетов. Тогда в одной минуте — 5292000, а в 4 минутах (типичная длительность композиции) — 21168000 отсчетов. В качестве примера средствами Cubase SX мы проанализировали спектр 4-минутной композиции. На нашем компьютере для этого понадобилось 10 секунд. При этом было выбрано число отсчетов, равное 4096 (что для анализатора спектра Cubase SX в два раза меньше максимального). Если бы программа использовала для вычислений все отсчеты, которыми представлена композиция (более 21 миллиона отсчетов), то для решения этой задачи ей потребовалось бы непрерывно работать больше 14 часов. Существуют аудиоредакторы, позволяющие не только анализировать текущий и мгновенный спектры, но также и редактировать звуковой сигнал, представленный в спектральной форме. Примером подобной программы может служить аудиоредактор Cool Edit Pro 2. Конечно, от такой универсальной программы, как Cubase SX, нельзя требовать, чтобы она позволяла обращаться со спектром так же свободно, как и специализированный звуковой редактор. Вместе с тем, в Cubase SX возможности для проведения спектрального анализа все же имеются.

Измерение спектра в Cubase SX

Команда, инициализирующая анализатор спектра, имеющийся в Cubase SX, доступна только при следующих условиях: в проекте существует хотя бы один аудиотрек, на треке имеются аудиоданные и выделен хотя бы фрагмент части с аудиоданными. Для выделения фрагмента нажмите кнопку в окне Cubase SX Project, затем нажмите левую кнопку мыши и проведите курсором мыши от одной границы предполагаемого выделения до другой. После этого отпустите кнопку мыши. Для выделения всей части сделайте на ней двойной щелчок левой кнопкой мыши. Если хотя бы один трек выделен при нажатой кнопке , то спектральный анализ будет автоматически проводиться поочередно на каждом треке.
Доступ к анализатору спектра в Cubase SX осуществляется из главного меню командой Audio > Spectrum Analyzer. Этой командой отрывается диалоговое окно Spectrum Analyzer (рис. 1.27), предназначенное для выбора режима спектрального анализа.
В окне диалога Spectrum Analyzer имеются следующие опции:

* Size in Samples — объем выборки (число отсчетов, на основе которых будет выполняться БПФ). Чем больше число, выбранное в этом поле, тем точнее анализ и тем больше времени потребуется для его проведения.
* Size of Overlap — степень наложения блоков выборок в процессе спектрального анализа. Оптимальное значение этого параметра устанавливается автоматически при изменении числа в поле Size in Samples. В любом случае значение данного параметра должно быть меньше, чем значение параметра in Samples. Если попытаться задать значения Size of Overlap и Size in Samples равными, то программа закроется без всякого предупреждения и сохранения текущего проекта в файле.
* Window used — раскрывающийся список для выбора вида спектрального окна.
* Normalized values — флажок включения нормализации полученных значений. При установленном флажке наибольшее значение спектральной функции будет приравнено к уровню 0 дБ или к значению 1.
* From Stereo — раскрывающийся список для выбора режима обработки стереосигнала. Возможные варианты: анализ монофонического сигнала, полученного суммированием сигналов правого и левого каналов, анализ сигнала левого канала, анализ сигнала правого канала, раздельный анализ сигналов каждого из стереоканалов (спектры отображаются графиками, которые отличаются цветом).

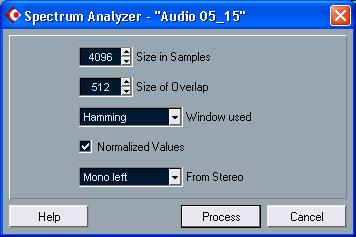
Рис. 1.27. Окно Spectrum Analyzer для выбора параметров анализа спектра
Когда вы нажмете кнопку Process, начнется спектральный анализ выборки сигнала, находящейся в выделенном фрагменте. Будет вычисляться спектр. Спустя некоторое время расчет спектра завершится и откроется окно с графиком спектра (рис. 1.28).
Обладая некоторым опытом общения с анализатором и профессиональным чутьем, по спектру сигнала вы сможете, например, разыскать на графике даже небольшой выброс, в котором сосредоточена основная энергия помехи. Затем с помощью фильтра можно удалить этот выброс из спектра сигнала, существенно улучшив при этом отношение полезного сигнала к шуму.
Если окно с графиком спектра покажется мелковатым, вы можете увеличить его традиционным способом с помощью мыши.

Рис. 1.28. Окно Spectrum Analyzer с результатами анализа спектра

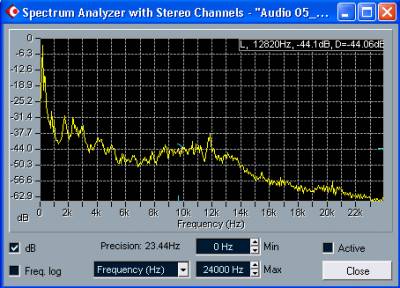
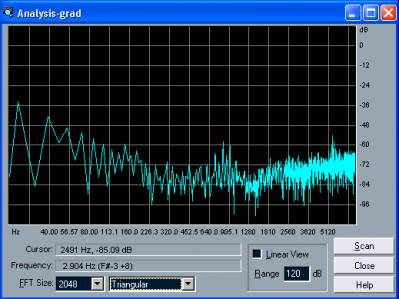
Рис. 1.29. Спектр сигнала при логарифмическом масштабировании оси частот
А теперь рассмотрим график внимательнее. По горизонтальной оси откладывается частота в герцах, по вертикальной — уровень компонентов сигнала на этой частоте.
Если флажок dB установлен, то значения спектральной функции откладываются в логарифмической шкале, оцифрованной в децибелах, если сброшен — в линейной шкале (либо ненормированной, либо нормированной к единице).
При сброшенном флажке Freq. log горизонтальная ось размечается в линейном масштабе, в котором удобнее рассматривать весь спектр в целом, включая и его высокочастотную область. Если этот флажок установлен, то по горизонтали назначается логарифмический масштаб. Логарифмический масштаб позволяет в деталях наблюдать низкочастотную часть спектра. Для сравнения на рис. 1.29 при логарифмической шкале по оси частот показан спектр того же самого сигнала, для которого на рис. 1.28 выбран линейный масштаб.
Справа вверху располагается поле, в котором отображаются данные о'значениях спектральной функции сигналов правого и левого канала для той частоты, на которую в данный момент указывает курсор мыши. Сама частота также отображается в поле. Сказанное справедливо при условии, что курсор находится в пределах координатного поля. При перемещении курсора значения параметров изменяются. Если курсор находится вне пределов координатного поля, то значения отображаемых параметров не меняются, причем они соответствуют той частоте, при которой курсор, покидая координатное поле, пересек его границу.
Обратите внимание на то, что числа, отображаемые в поле, не являются координатами курсора мыши. В этом поле вы видите координату курсора мыши на оси частот и соответствующее ей значение спектра. Это упрощает процесс численного измерения значений спектральной функции. Вам не нужно прицеливаться в конкретную точку на координатной плоскости. Достаточно добиться, чтобы в поле появилось искомое значение частоты, а значение спектра для нее программа предъявит вам автоматически. Точка на графике, которой соответствуют числа, отображаемые в поле, выделяется зеленой окружностью, а проекции этой точки на координатные оси отмечаются зелеными черточками.
Возможно, вам понадобится рассмотреть в подробностях поведение спектральной функции на каком-либо ее конкретном участке. В полях Min. и Мах. вы можете задать нижнюю и верхнюю границы частотного диапазона, отображаемого в окне.
В поле Precision: программа отображает значение разрешающей способности измерения спектра, которая зависит от объема выборки (см. поле ввода Size in Samples на рис. 1.27).
В единственном раскрывающемся списке выбирают один из двух вариантов оцифровки горизонтальной оси координат:

* Frequency (Hz) — в традиционных единицах измерения частоты (герцах).
* Note (С) — "в нотах". Вместо значений соответствующих частот шкала будет размечена символами С0, C1, C2, ..., С10, которые означают ноты до различных октав (например, до пятой октавы соответствует частоте 523,251 Гц).

При установленном флажке Active всякий раз, когда вы станете выбирать команду Audio > Spectrum Analyzer, очередной график с результатами анализа будет отображаться в том же самом окне (заменяя собой предшествующий график). Если флажок сброшен, новые результаты спектрального анализа появятся в отдельных окнах. Последний режим очень удобен, так как позволяет сравнивать спектры сигналов, записанных на различных треках, что чрезвычайно важно при обработке отдельных музыкальных партий фильтрами в процессе сведения композиции.

Анализ спектра и фильтрация при сведении композиции

Раз уж мы заговорили о сведении, то упомянем о том, что оно включает в себя несколько этапов:
1. Индивидуальный контроль отсутствия ошибок в партии каждого инструмента.
2. Перезапись партий в исполнении MIDI-инструментов (если таковые есть в композиции) на аудиотреки.
3. Выставление ориентировочного баланса уровней всех партий и предварительное панорамирование.
4. Корректировка частотных характеристик партий.
5. Динамическая обработка звуковых сигналов.
6. Обработка эффектами.
7. Динамическое изменение уровня аудиосигнала каждого трека (в каких-то местах каждая партия должна звучать несколько громче, в каких-то — тише).
8. Уточнение относительных уровней, уточнение распределения партий по панораме.
Сейчас речь идет о спектральном анализе, поэтому остановимся лишь на четвертом этапе: коррекции частотных характеристик партий. С помощью эквалайзеров нужно добиться гармоничного сочетания всех партий. Сделать так, чтобы в звучании каждого инструмента присутствовали характерные тембры и, вместе с тем, чтобы, по возможности, их спектры не перекрывались: энергия сигналов равномерно распределялась бы в пределах звукового диапазона частот. Только в этом случае удастся добиться прозрачности звучания композиции. Начинать такую работу нужно со спектрального анализа сигналов каждого из треков в отдельности. Для того чтобы наглядно пояснить то, о чем сейчас идет речь, рассмотрим простой пример. Пусть имеется три трека и требуется их сбалансировать по тембру. Проведем спектральный анализ каждого трека с помощью Spectrum Analyzer, причем флажок Active сбросим. Полученные графики спектральных функций представлены на рис. 1.30.

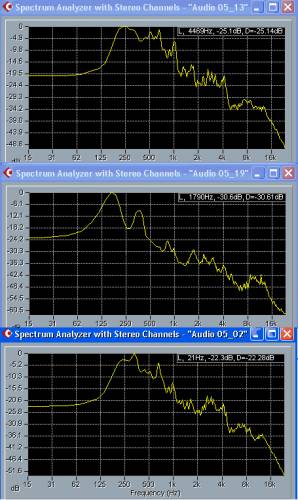
Рис. 1.30. Результат спектрального анализа аудиосигналов на трех треках
Разработчики Cubase SX не приводят детальных сведений об алгоритме спектрального анализа, реализованного в программе. Поэтому в процессе работы над книгой мы решили провести сравнение полученных результатов с теми, что дает какой-либо другой виртуальный анализатор спектра. В качестве альтернативного мы выбрали анализатор спектра программы Cool Edit Pro 2, детально описанный нами в книге [10]. Анализировались одни и те же тестовые сигналы, спектры которых были нам заранее известны, т. к. их описание имеется в научных литературных источниках. Также проводился анализ сигналов, полученных путем перезаписи на аудиотреки MIDI-инструментов. По результатам этого эксперимента можно сделать следующие выводы.
1. Анализатор спектра Cubase SX дает большую погрешность на частотах ниже 40—50 Гц. Создается впечатление, что в этом диапазоне существует некий порог чувствительности измерителя. Об этом косвенно свидетельствует такой, например, результат: сигнал на треке № 3 (нижний график на рис. 1.30) был обработан фильтром, ослабившим все частоты в диапазоне 0—50 Гц на 30 дБ. На слух результат такой обработки заметен хорошо: из звучания рояля исчез призвук, похожий на слабые удары по бас-барабану, который в необработанном сигнале слышен в моменты нажатия клавиш. Однако спектральный анализ отфильтрованного сигнала средствами Cubase SX показал, что уровень спектральной функции остался прежним (все те же -26 дБ), хотя должен был бы снизиться до -56 дБ. Причиной этого может быть ограниченное время анализа. Кроме того, даже при наибольшем числе анализируемых отсчетов (Size in Samples) разрешающая способность анализатора спектра Cubase SX составляет около 6 Гц, а график всего рассматриваемого низкочастотного участка спектра строится лишь по 8—10 точкам. Анализатор спектра программы Cool Edit Pro 2 "заметил" понижение уровня низкочастотных составляющих фильтром.
2. Анализатор Cubase SX вычисляет спектр либо на участке трека, выделенном при нажатой кнопке , либо на всем треке (поочередно на каждом треке, если хотя бы один трек выделен при нажатой кнопке ). Иными словами, измеряется мгновенный спектр, поэтому вид графика спектра зависит от расположения и протяженности выделенного фрагмента.
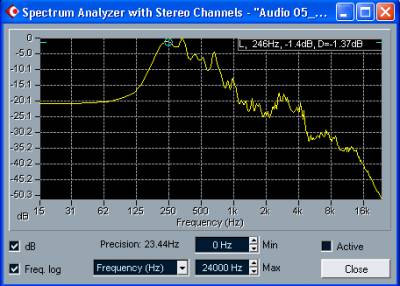
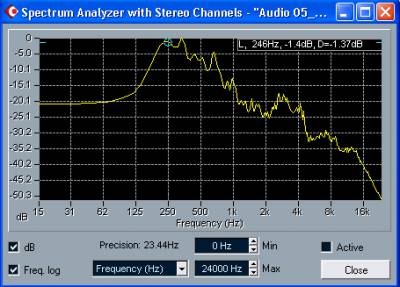
3. Анализатор Cubase SX сглаживает разброс между значениями соседних локальных максимумов и минимумов спектральной функции. Чтобы убедиться в этом, достаточно сравнить рис. 1.31 и 1.32. На первом из рисунков показан спектр, измеренный анализатором Cubase SX, на втором — Cool Edit Pro 2. Анализируется один и тот же сигнал. В результате подобного сглаживания пользователю нетрудно допустить ошибку в оценке того, какие спектральные компоненты аудиосигнала следует считать существенными, а какие — нет, так как создается субъективное впечатление, будто значения спектральной функции с ростом частоты уменьшаются быстрее, чем это происходит на самом деле.

Рис. 1.31. Спектр сигнала, измеренный средствами Cubase SX

Рис. 1.32. Спектр сигнала, измеренный средствами Cool Edit Pro 2
А теперь возвратимся к рис. 1.30 и рассмотрим его сверху вниз.
На треке № 3 записана партия баса, на треке № 2 — аккомпанирующего инструмента, на треке № 1 — солирующего инструмента. Результаты спектрального анализа соответствуют такому распределению инструментов. Спектр сигнала на треке № 3 сосредоточен в основном в области частот 20 Гц - 400 Гц, на треке № 2 - 60 Гц - 2 кГц, на треке № 1 - 60 Гц - 8 кГц.
Напрашивается такая последовательность обработки сигналов частотными фильтрами:

* к треку № 3 можно применить фильтр нижних частот с частотой среза 400 Гц для того, чтобы полностью подавить высокочастотные составляющие. Уровень передачи сигнала в полосе подавления фильтра можно установить порядка -30 дБ — -40 дБ (или минимально возможный для эквалайзера, имеющегося в вашем распоряжении);
* на треке № 2 можно без потери качества подавить спектральные составляющие, лежащие ниже 60 Гц. Для этого сигнал следует обработать фильтром верхних частот с частотой среза 60 Гц. Кроме того, фильтром нижних частот можно подавить спектральные составляющие, расположенные выше 2 кГц — 3 кГц;
* на треке № 1 полосно-подавляющим фильтром можно ослабить на 10 дБ — 15 дБ спектр в полосе частот 500 Гц — 1,5 кГц (приблизительно). Это позволит устранить маскировку звука аккомпанирующего инструмента, записанного на треке № 2.

В целом после такой обработки фильтрами уменьшится уровень нелинейных искажений в области нижних частот, а в звучании композиции появится прозрачность.
Заметим, что рассмотренный вариант фильтрации — не единственный. В зависимости от поставленной цели можно попытаться реализовать несколько различных стратегий обработки фильтрами сигналов, имеющих такие спектры. Анализатор спектра лишь помогает сориентироваться, а контролировать качество звука, полученного в результате фильтрации, следует только на слух.